Способы задания движения точки

КИНЕМАТИКА ТОЧКИ
Способы задания движения точки
Существуют три способа задания движения точки………

Способы задания движения точки

Существуют три способа задания движения точки.

Векторный способ.
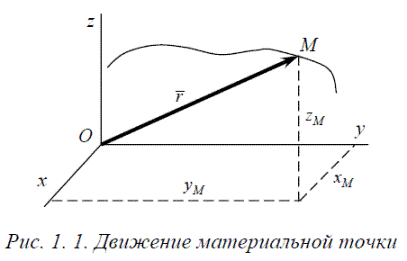
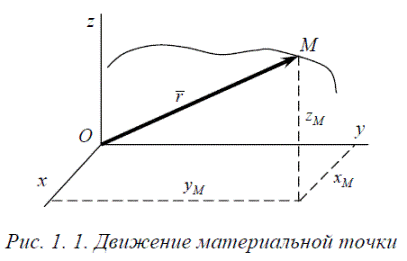
Положение точки определяется радиус-вектором (рис.1.1), проведённым в данную точку из неподвижного начала отсчёта.
r = r (t) ≡ OM (t).
С течением времени радиус-вектор будет изменяться, поэтому он является некоторой заданной векторной функцией времени r = r (t) . Это уравнение называется уравнением движения точки в векторной форме.
Непрерывная кривая, с точками которой в каждый момент времени совпадает движущаяся точка, называет траекторией. По отношению к различным системам отсчёта точка будет описывать разные кривые. Следовательно, траектория относительное понятие.
Геометрическое место концов переменного вектора называется годографом. Таким образом, траектория точки есть годограф радиусвектора этой точки.

Координатный способ.
Положение движущейся точки относительно выбранной системы отсчёта определяется её координатами в каждый момент времени (рис. 1.1): x = f1 t , y = f2 t , z = f3 t .

Функции f1 t , f2 t , f3 t . должны быть однозначными, непрерывными и, по крайней мере, дважды дифференцируемыми. Уравнения движения точки в координатной форме можно рассматривать и как уравнения траектории в параметрическом виде. Если исключить из этих уравнений параметрt , то получим уравнение траектории, как пересечение двух поверхностей
F1 (x, y) = 0, F2 (y, z) = 0.

Естественный способ.
Если известен вид траектории, то движение точки удобно задать естественным способом (рис. 1.2). Для этого на траектории назначают начало отсчёта (точка О), направление отсчёта и записывают зависимость дуговой координаты s от времени t

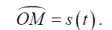
Функция s = s (t) по самой природе механического движения должна быть непрерывной и однозначной.

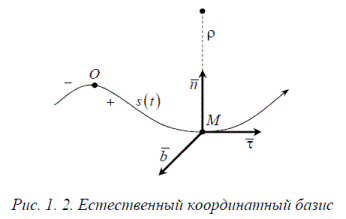
С траекторией точки можно связать естественный координатный базис: единичные векторы касательной — 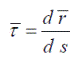главной нормали — 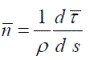и бинормали к траектории 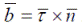. Здесь ρ — радиус кривизны траектории.
Эти три вектора образуют естественный репер, вдоль них идут естественные оси. Координатные плоскости образуют сопровождающий трёхгранник и носят названия: плоскость (τ ,n ) — соприкасающаяся, плоскость ( n ,b ) — нормальная, плоскость (b ,τ ) — спрямляющая.